Residual Variance in principal component space qualitative model

Submitted by marta on 1 October 2013 - 12:37pm
Hi All
I developed a qualitative identification method (Library) to identify pharmaceutical finished product (Capsules).
In the library there are two products :the product itself 479 spectra, the product placebo 16 spectra.
The pattern recognition method used is "Residual Variance in principal component space"
The match value used: Probability level: 0.95 (Samples with lower probability than 0.95 pass identification)
Pretreatment (SNV+2nd derivative)
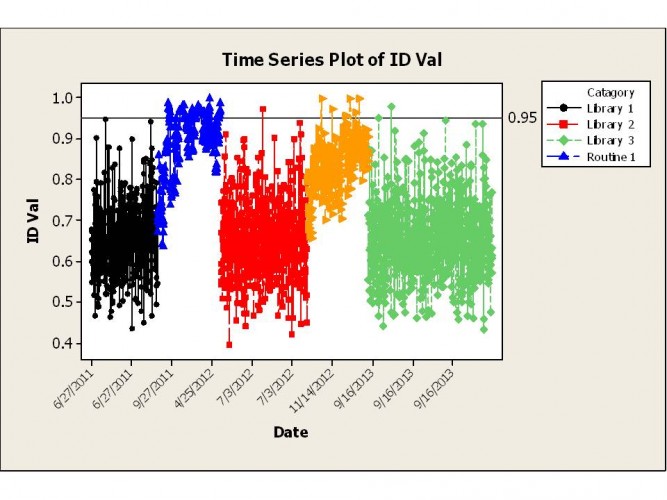
The problem is that each time I deploy my method the probability values obtained immediately increase and much higher values are obtained during routine use than during internal validation. (See picture added)
The black, red and green points show the values for internal validation for the model updated with the spectra from routine analysis
Can any of you out there think of acause for this
Thanks
.
jcg2000
01 Oct 2013
Hi Marta:
The method you posted here spans more than 2 years. Good chance is that the calibration samples no longer represent the samples you used for routine analysis. Have you updated the library by inlcuding authenticated routine samples?
The pattern recognition method you used is very sensitive to variance in spectral measurements and sample variations. Make sure you use the same sample presentation method as you developed the model.
For material identification, a more robust pattern recognition method would be correlation coefficient among spectra. If you have to differentiate between product and the placebo where the spectral difference is subtle, you can select the wavelength ranges where you do see the difference between product and placebo. Hopeful that could lead to a model that is more resistant to variance in samples and instrument.
Jerry Jin
Permalink
jjakhm
01 Oct 2013
Marta,
One thing to note is that the number of routine test samples exceeding 0.95 seems to have dropped from the first deployment to the second. This could indicate an issue regarding a disparity between variations trained into the model and that observed of new samples (it is possible that enough variation has not been captured in the model yet since significant variation spans a broader time interval. This could be sample related or measurement related). Over what period of time was the initial calibration data collected? From the plot it appears that the data was collected primarily on one day in june-2011 (unless this date represents something like when the data was added to a database/library and not the actual collection date). I would echo the sentiments concerning sample presentation, measurement conditions, environmental conditions, etc. I don’t necessarily agree that the correlation coefficient method is more robust as I believe it is application dependent.
What do the predicted sample and calibration sample residuals look like and does a pattern evolve over time? The same could be asked about the scores. It also appears that the number of samples exceeding 0.95 in the second deployment is in line with what is to be expected from a 0.95 probability level (~5 or 6 samples among several hundred?)…Although the trend is still something to be concerned with I suppose. The 0.95 probability level is arbitrary, does the software allow changing it and can you justify increasing this value? If you check an F-test table you will notice that the critical F-ratio approaches 1 as the degrees of freedom go to infinity. You can reduce the sensitivity of the test by selecting fewer samples for your calibration model while still sampling the space appropriately (increase the critical F-ratio while spanning an equivalent space of variation). I believe this can be achieved using a sample selection algorithm like Kennard-Stone or similar approach (if it does not impact the number of false positives to a degree that you are approving an unacceptable quantity of “bad” samples… maybe there are other posts regarding this topic, but I’m not sure.). If there is an issue, implementing the two prior suggestions may only prolong the amount of time until recalibration and validation are required. However, the concept of an issue is relative and some may have the opinion that this process is largely normal and should just be addressed as a part of routine maintenance/periodic recalibration/revalidation as certain applications are inherently more prone to this type of frequency.
Best Regards,
Jason
Permalink